Prime numbers, like $2, 5 7,$ and $47$ are special ¹. Unlike say 4 = 2 * 2 or 33 = 3 * 11, prime numbers can’t be written as the product of other numbers. They’re the fundamental block we express other numbers through: every natural number, 1, 2, 3, … is the product of primes ². How many of these special prime numbers are there?

Infinitely many! A recent one-line proof by Sam Northshield shows why there are infinitely many primes ³:

$$0 < \prod_p \sin(\pi / p) = \prod_p \sin(\frac{\pi * (1 + 2 * \prod_{p\prime} p\prime)}{p}) = 0.$$

You may wonder how sin relates to prime numbers. Why $\pi$? Why is the left less than the right?

In this post, we’ll untangle this elegant, one-line proof to reveal the answers.

Imagine

Let’s imagine there’s a fixed number of primes. What then?

Ignoring the in-between, the proof says

$$0 < \text{something} = 0.$$

This means “something” is simultaneously equal to zero and strictly less than zero. What we imagined—that there’s a fixed number of primes—is then impossible. There must be infinitely many primes.

Now let’s untangle the “something” in between.

Step 1: $0 <$ “Something”

First, let’s understand what these symbols mean:

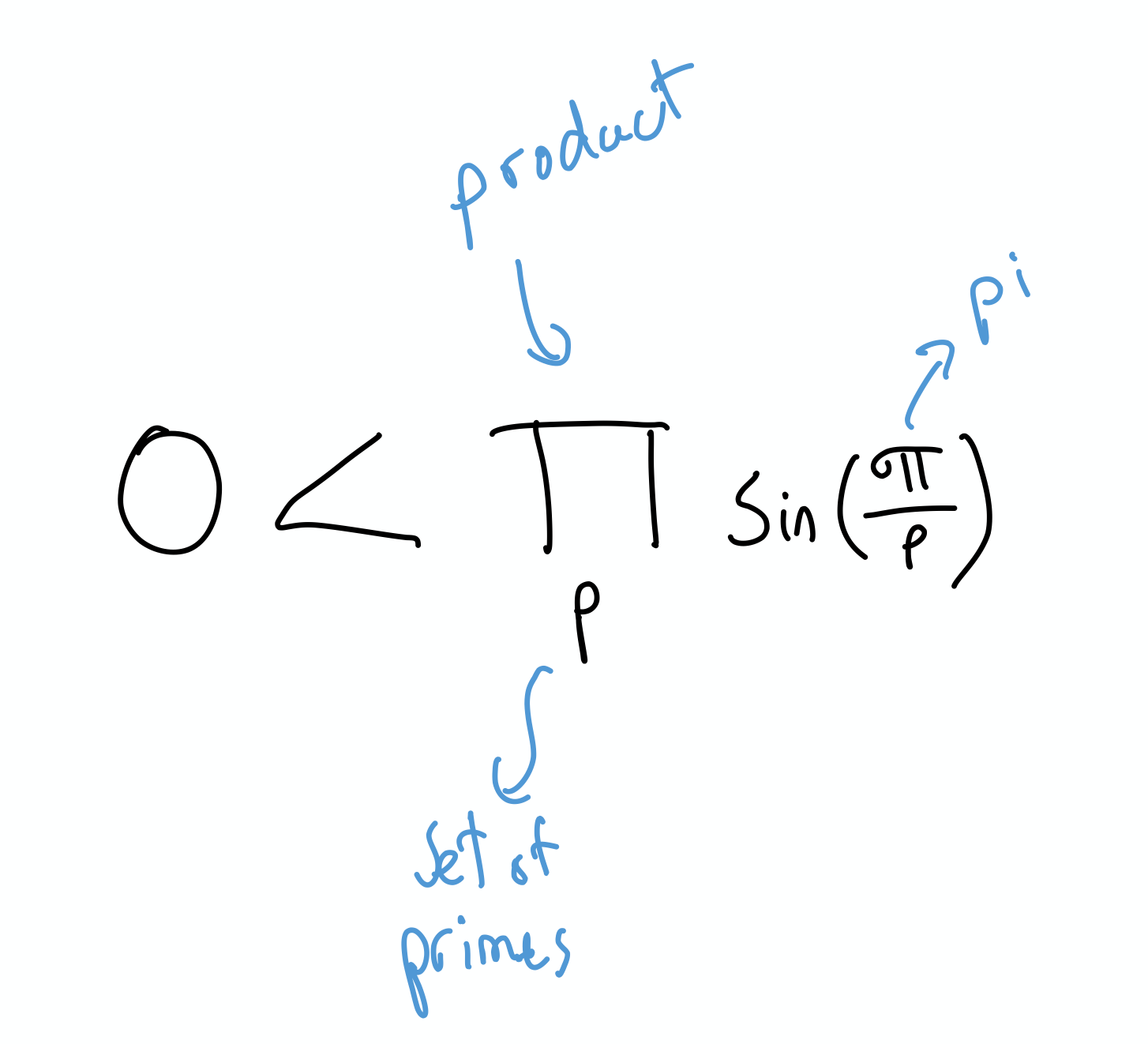
• Careful, pi = 3.14… and product look very similar.

How do we know “something” is greater than zero?

Let’s see what these values equal

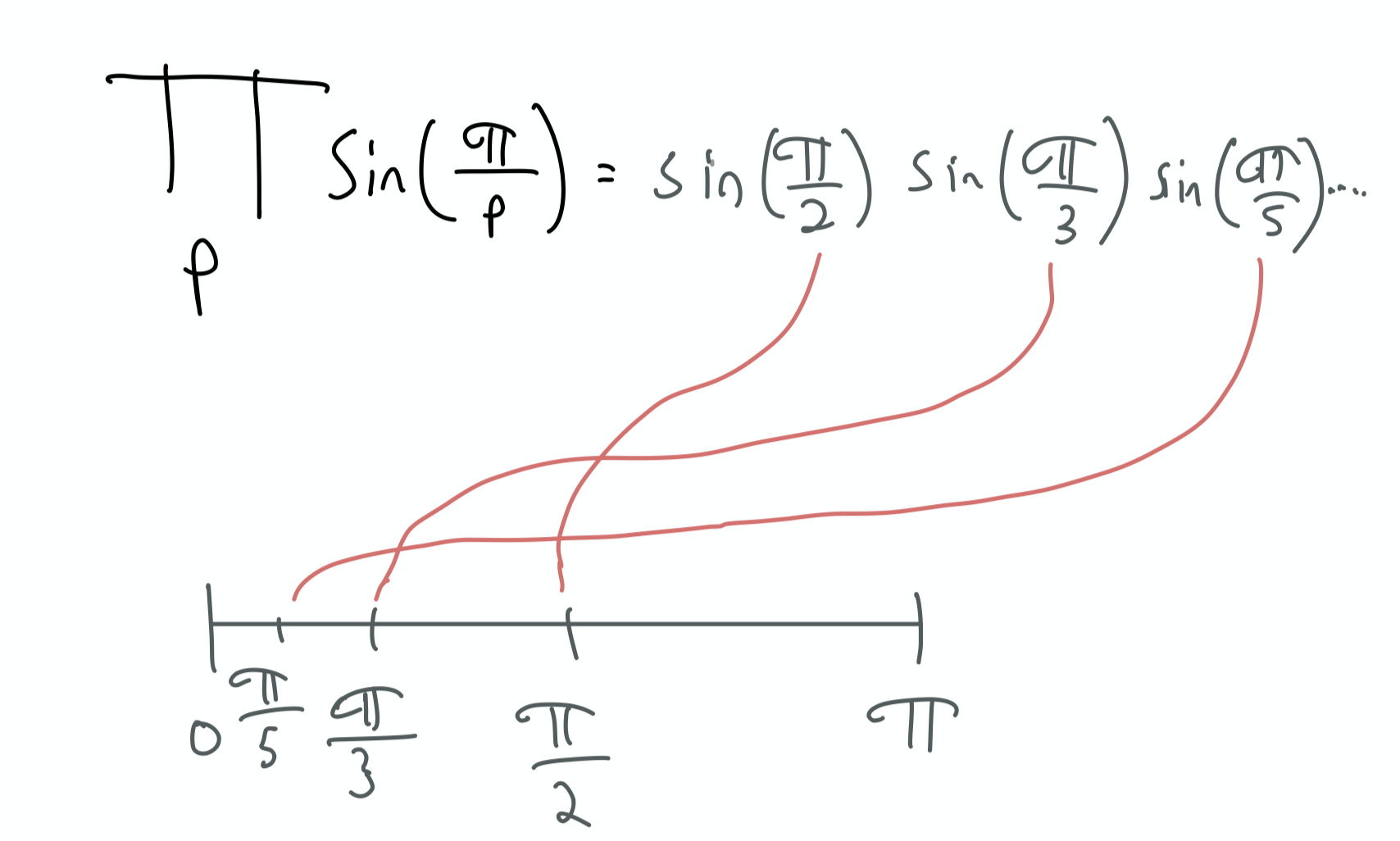
Not matter which prime $p$ we choose, $sin(\pi / p) > 0$.

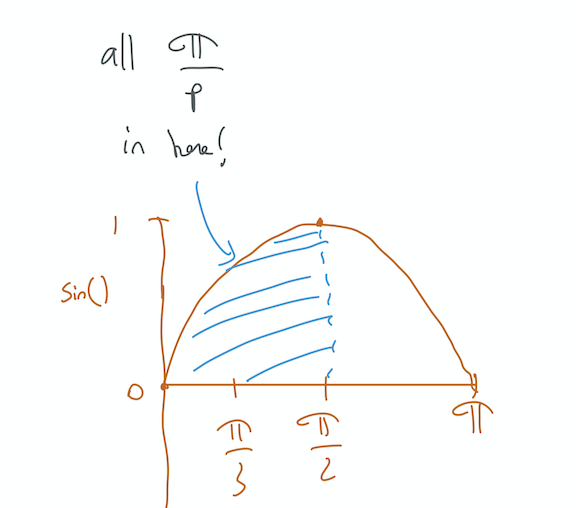
This means “something” is the product of positive numbers. “Something” $= \prod_p sin(\pi / p) = + + …+ = +$.

“Something” must be greater than 0.

Step 2: Rewrite “Something”

We want to rewrite “something” in a new form to see it’s also equal to zero. The proof says

$$\sin(\pi / p) = \sin(\pi / p + 2 \pi \prod_{p\prime} p\prime/ p).$$

The product inside sin means

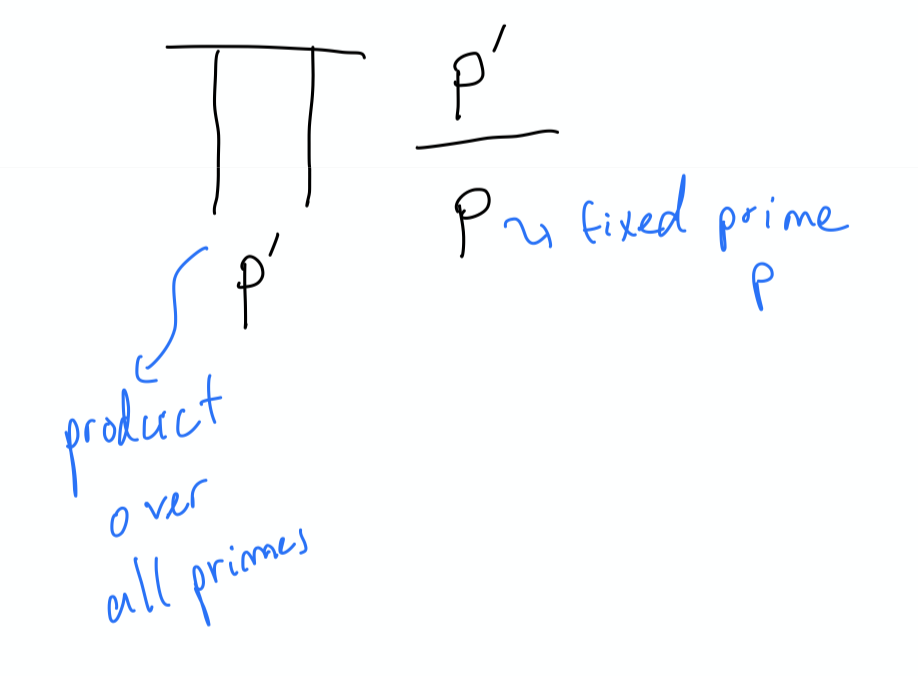
Let’s look at a graph of sin

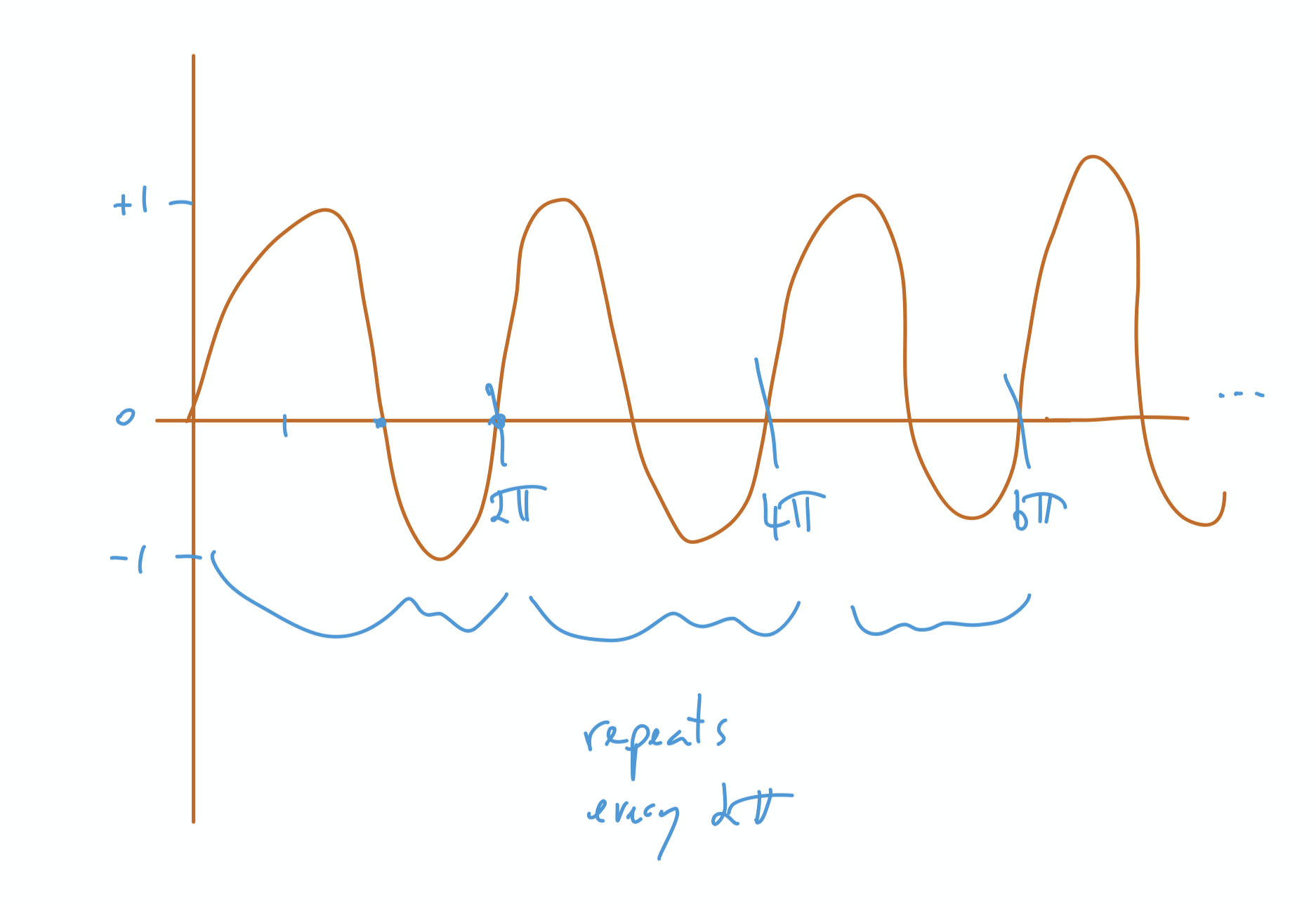
The graph between 0 and $2\pi$ is exactly the same as that between $2\pi$ and $4\pi$. It’s a repeating pattern every $2 \pi$. The pattern says

$$\sin(n) = sin( n + 2 \pi \#)$$

for any # $0, 1, 2, \dots$.

Let’s think about one case when $p = 5$. Remember we know

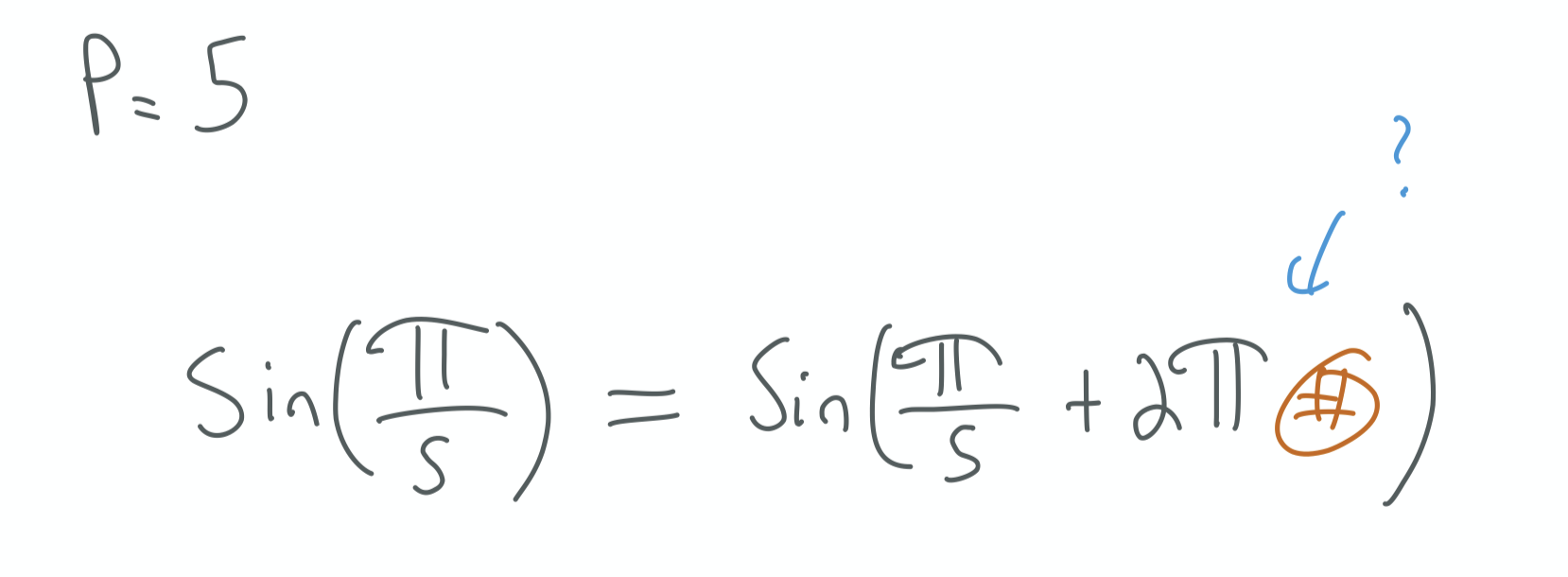
no matter which orange # we choose.

What if we choose the # to be $\prod_{p \prime} \frac{p\prime}{5}$?

Using the repeating pattern of sin we can then rewrite $\sin(\pi / 5)$ as

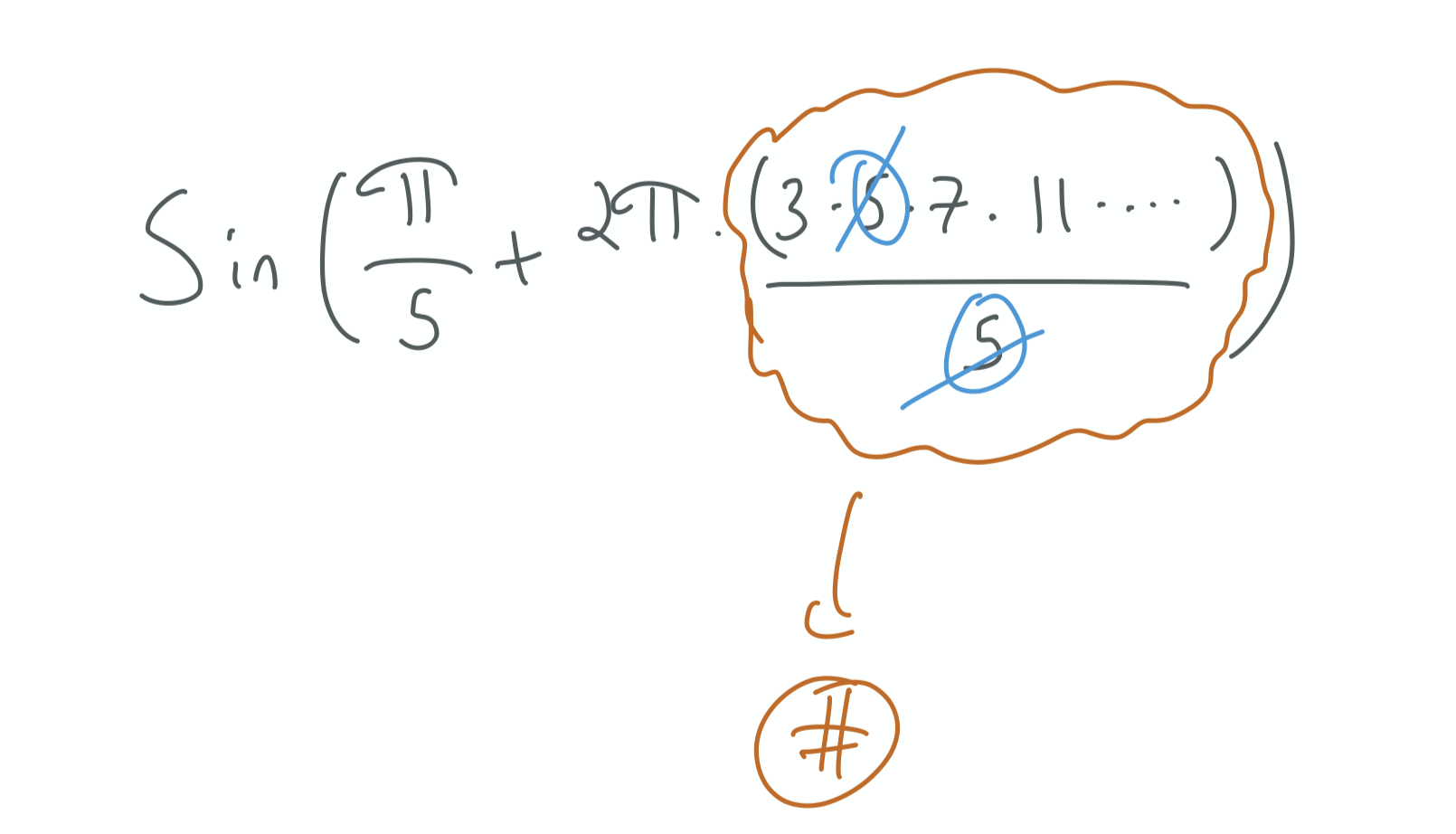
Luckily, this is true not just for $p=5$, but for any $p$. We can always find a $p \prime$ in the numerator to cancel $p$. For any $p$, we then get

$$\sin(\pi / p) = \sin(\pi / p + 2 \pi \prod_{p\prime} \frac{p\prime}{p}).$$

Step 3: “Something” equals 0

Finally, let’s see why “something” = $\prod_p sin(\pi / p)$ is also zero. Let’s look at where sin is zero

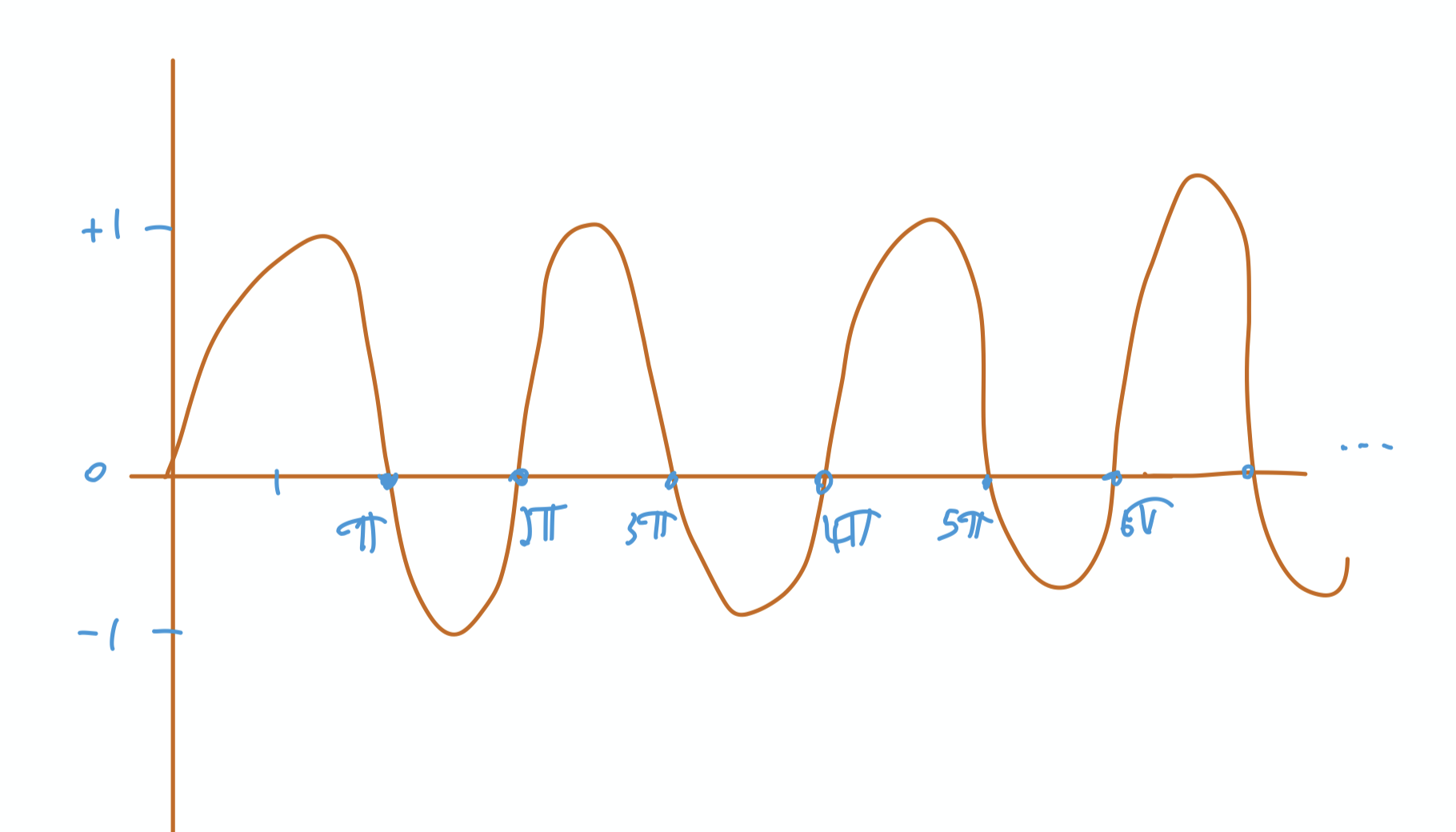
$sin(k \pi) = 0$ for any $k = 0, 1, 2, …$.

Let’s rewrite the terms inside sin in a friendlier form:

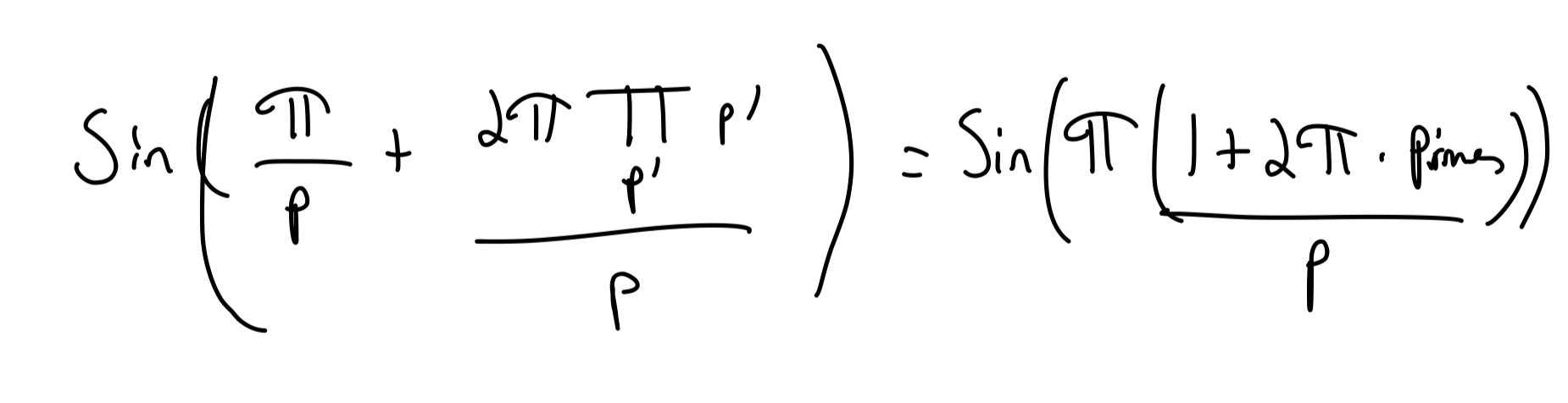
by combining the terms under a common denominator.

Now notice

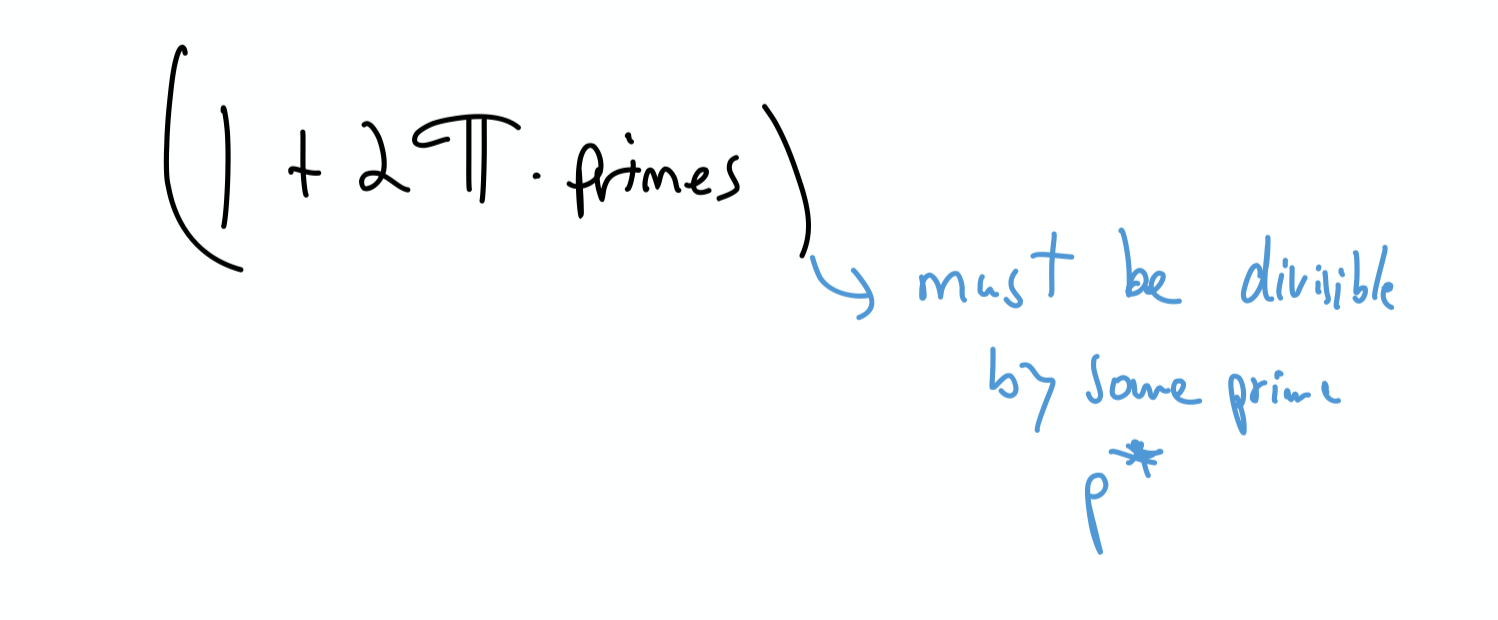
because every natural number can be written as the product of primes.

Let’s call one of those primes $p^*$. Then,

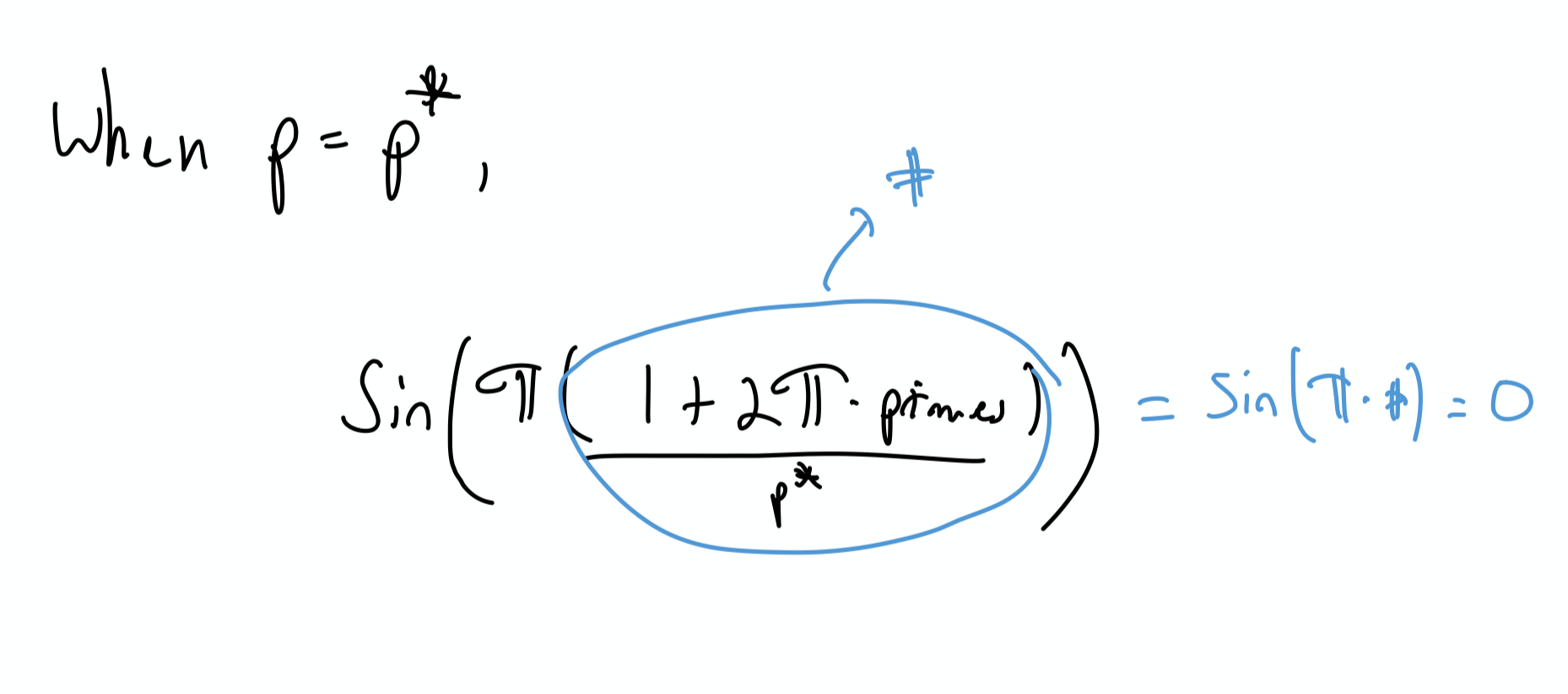
Now we have one term in our product that’s zero (when $p = p^*$), meaning

$$\prod_p \sin(\pi / p) = \sin(\pi / 2) \sin(\pi / 3) * 0 * .... = 0.$$

The Punch Line

If we assume there are finitely many primes,

$$\prod_p \sin(\pi / p) = 0,$$

and from step 1

$$\prod_p \sin(\pi / p) < 0.$$

That can’t be.

We confidently conclude our original assumption is wrong. There must be infinitely many primes.

1. prime numbers are also special in an everyday sense. Finding these special numbers is what makes sending credit card info. on the internet secure ↩

2. natural numbers are 1, 2, 3, 4, …. excluding fractions or irrational numbers such as pi. ↩

3. Many other proofs exist showing there are infinitely many primes (see prime factorization). ↩